
Spela Futoshiki pussel Online
I följande handledning presenteras grundläggande och avancerade tekniker för att lösa Futoshiki-pussel steg för steg, med tillhörande illustrationer för att visa upp metoderna på specifika kortkonfigurationer.
Utgångspunkten för att nå en lösning är definitionen av själva spelet: Futoshiki kräver att användaren tar reda på ett bräde där varje siffra visas en gång på varje rad och kolumn, genom att respektera brädans ojämlikheter. Genom att använda detta kriterium, framsteg mot en lösning kan göras genom att steg för steg fylla i tomma brädor med specifika siffror eftersom de är det enda sättet att respektera styrelsens begränsningar.
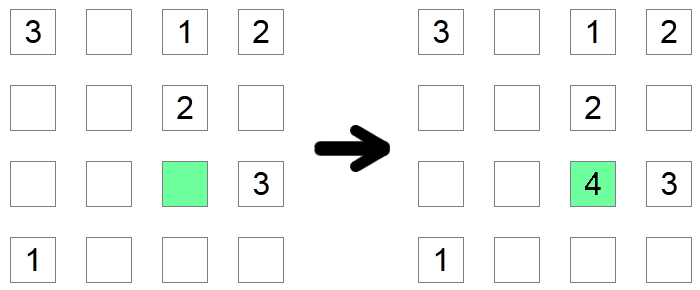
Om en fyrkantig kolumn och rad redan innehåller alla möjliga siffror, utom en, måste den fyrkanten innehålla den saknade siffran. I exemplet ovan måste den gröna rutan vara 4 eftersom det inte skulle tillåtas ha något annat värde eftersom de andra möjliga siffrorna redan finns i raden eller kolumnen.
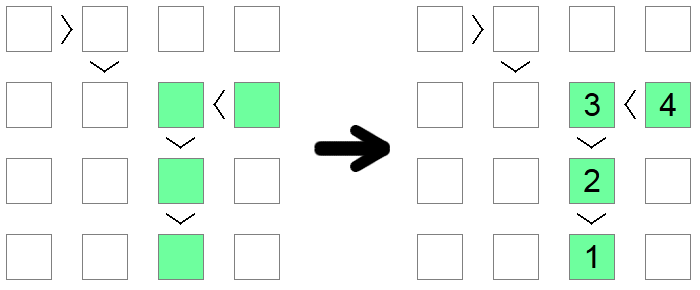
Om du märker en kedja av ojämlikheter, vare sig det är antingen < (alla stigande) eller > (alla fallande), lika i storlek med brädans storlek, då måste kedjan vara en sekvens från 1 upp till längden på brädet. Kedjans längd garanterar att denna sekvens är den enda möjliga lösningen som uppfyller det monotona villkoret som ojämlikhetskedjan ålägger.
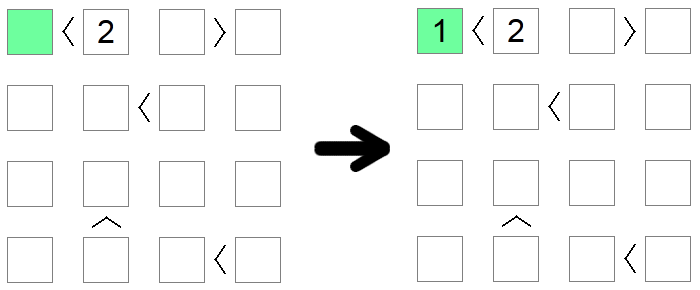
Kvadrater som är mindre än 2 måste implicit ha värdet 1 eftersom det är det enda tillåtna värdet på brädet som respekterar detta villkor. På samma sätt måste rutor som är större än brädstorleken minus 1 vara lika med brädstorleken. I exemplet ovan är det enda möjliga värdet för den gröna rutan (mindre än 2) 1.
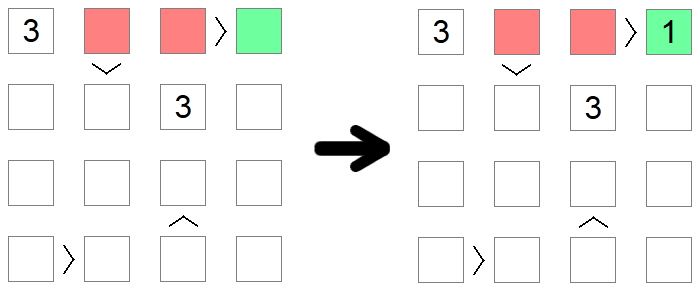
Kvadrater som är större än andra rutor kan inte vara 1, det lägsta tillåtna värdet på brädet, eftersom det inte finns något värde mindre än 1. Liknande, rutor som är lägre än andra rutor kan inte innehålla det högsta tillåtna värdet, eftersom det inte skulle finnas något större att fylla på andra sidan ojämlikheten. I exemplet ovan kan 1 inte fyllas i de röda rutorna eftersom de alla är större än andra brädrutor, så den enda möjliga placeringen för 1 på brädans första rad är den gröna fyrkanten.
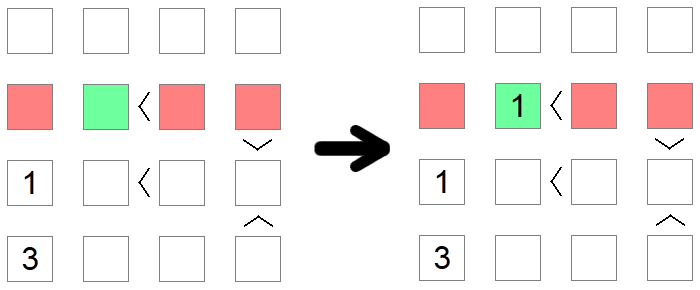
Ibland måste flera regler användas för att nå en slutsats. Detta är fallet i exemplet ovan, där vi försöker placera värdet 1 på brädans andra rad. Den första röda fyrkanten elimineras på grund av en kolumnuteslutning (vi har redan en 1 på den kolumnen), medan den andra och tredje röda rutan elimineras på grund av en uteslutning av minvärden eftersom dessa platser har större än ojämlikheter associerade med dem. Därför förblir den gröna torget den enda möjliga platsen för att placera 1 i den raden.
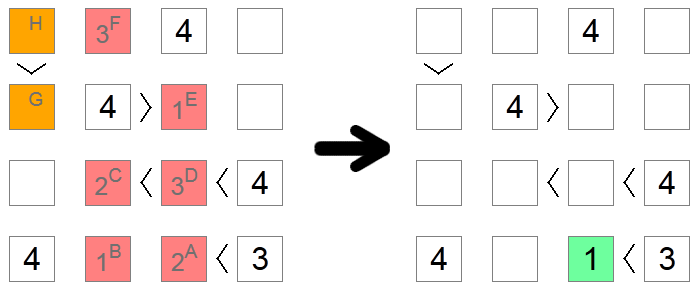
Ibland, särskilt på svåra brädor, det finns inga andra sätt att räkna ut rätt siffra för en kvadrat förutom att dyka in i konsekvenserna av varje möjlighet tills en motsägelse uppnås. I exemplet ovan är alla röda och orange rutor initialt tomma. Vi vill ta reda på om kvadrat A innehåller 1 eller 2. Vi antar att det innehåller 2 och vi kontrollerar om vi når en motsägelse baserad på detta antagande.
Om kvadrat A har en 2, skulle kvadrat B ha en 1 (det enda återstående värdet på den nedre raden). Kvadrat C kan vara 1 eller 2 eftersom det har en kedja av ojämlikheter som kräver att ha tillgängliga 2 större antal, men nu kan det inte vara 1 på grund av kolumnen uteslutning av kvadrat B, så kvadrat C är en 2, och kvadrat D är en 3 (det enda värdet mellan 2 och 4). På grund av kolumnuteslutningar, kvadrat E är 1 och kvadrat F är 3.
Om vi nu tittar på de orange rutorna märker vi motsättningen: om kvadrat G skulle vara 2, skulle kvadrat H behöva vara antingen 3 eller 4, som inte är tillåtna på grund av en raduteslutning. Om kvadrat G skulle vara 3, kvadrat H måste vara 4 vilket inte är tillåtet på grund av samma anledning. Eftersom vi inte längre har återstående värden för kvadrat G betyder det att vi nådde ett dödläge och vårt ursprungliga antagande var fel: 2 är inte ett giltigt drag för kvadrat A, så vi kan gå vidare och placera 1 i det, det enda andra möjliga värdet.
Vi har visat ovan hur man löser ett Futoshiki-pussel framgångsrikt genom att täcka en rad tekniker som kan hjälpa dig att härleda nästa drag även i svåra situationer. Den andra viktiga ingrediensen för att bli skicklig och snabb på att lösa Futoshiki-pussel är erfarenhet: ju mer du tränar, desto bättre och snabbare blir du.
Om du är ute efter en utmaning, du kan spela just nu ett slumpmässigt Futoshiki-pussel genom att klicka på knappen nedan. Lycka till!
© 2026 - Alla rättigheter förbehållna - Om - Sekretesspolicy - DE | EN | ES | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR